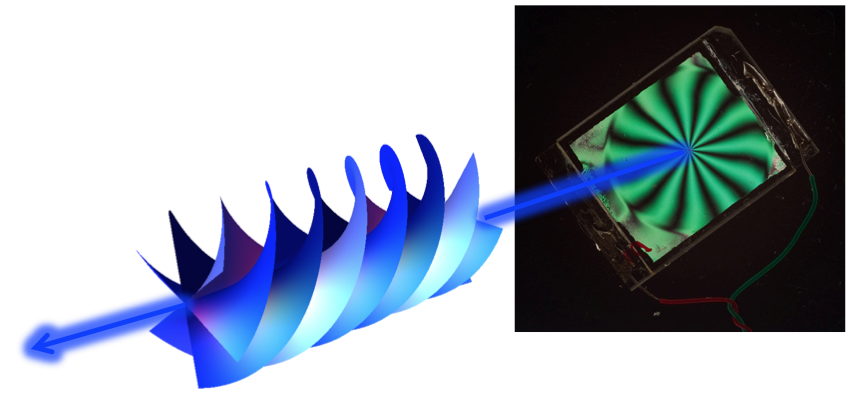
Abstract: A beam of light is characterized by the following local properties: intensity, phase, and polarization. In most practical cases, these optical properties are either uniform or varying in space in a smooth, simple fashion. But it is nowadays possible to create strongly space-variant light beams, in which one or more of these properties vary in space in a prescribed way, forming nontrivial geometrical patterns. In other words, it is possible to endow light with a geometrical “structure”. We will not be concerned here so much with the case of patterns of light intensity, which may be considered just as usual optical images. In my talk, I will mainly focus on optical patterns of phase and/or polarization. In contrast to intensity, which is defined as a nonnegative real number, phase and polarization can be represented as points in closed manifolds, e.g. a circle or a sphere. A pattern of these properties may then acquire a rich geometrical structure, including the possible appearance of topological singularities of different kinds, e.g. optical scalar vortices (singularities of phase) and vector-vortices (singularities of polarization), a multiple-helix shape of the optical wavefront, and other rather nontrivial three-dimensional structures of the light field. While conceiving these structures in theory is often very simple, realizing them in the lab is usually not as simple. There are today different tools allowing the experimenter to control the spatial structure of light. In my talk, I will mainly focus on a relatively recent invention for generating phase and polarization vortices and other structures exploiting a singular-patterned liquid crystal cell, commonly named “q-plate”. This name is due to the presence of a topological singularity of given charge “q” in the medium structure, exploiting the long-range orientational order that characterizes liquid crystals. Interestingly, even the working principle allowing this device to control the structure of light is somehow “geometrical” in its nature, being related to the so-called “geometric phase”, an ubiquitous concept crossing many boundaries of physics, ranging from optics to classical mechanics, to quantum mechanics.